Typical feature of some rectangles, including the Golden Rectangle

In a previous blog I showed that the golden rectangle is not so distinctive in its feature that when a square section is removed, the remainder is another rectangle with the same proportions as the first. Similarly, a feature of the "green rectangle" that I described is that when two square sections are removed, the remainder is another green rectangle with the same proportions as the first. This can be carried further, so that there exists a rectangle that when three square sections are removed, the remainder is another rectangle with the same proportions as the first.

Two quantities (positive numbers), a and b, are said to be in the golden ratio if (a+b)/a = a/b. In my previous blog I proposed that two quantities, a and b, be in the green ratio if (a+b)/(a-b) = a/b. The golden rectangle has been declared to be distinctive in that when b is removed from a, the ratio of b/(a-b) is the same as a/b. I showed that this feature is not so distinctive. That is because my green rectangle has the feature that when 2b is removed from a the ratio of b/(a-2b) is the same as a/b.

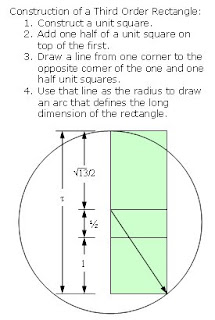
I will now define a new, "third order", rectangle whose side, a and b, are in the ratio of (a+b)/(a-2b) = a/b. If we define this ratio as τ, the Greek letter tau, this leads to:
τ² - 3τ - 1 = 0

The only positive solution to this equation is:
τ = (3 + √13)/2, or 6.606 (approximately).

Here's the calculation:

(a+b)/(a-2b) = a/b = τ

The right equation shows that a = bτ, which can be substituted in the left part, giving:

(bτ + b)/(bτ - 2b) = bτ/b

Canceling b yields:

(τ + 1)/(τ - 2) = τ

Multiplying both sides by (τ - 2) and rearranging terms leads to:

τ² - 3τ - 1 = 0

The only positive solution to this quadratic equation is:

τ = (3 + √13)/2 = approximately 3.303

A not so distinctive feature of the golden rectangle is that when a square section is removed, the remainder is another rectangle with the same proportions as the first. Similarly, a feature of the green rectangle is that when two square sections are removed, the remainder is another green rectangle with the same proportions as the first. Now I will show that a feature of the third order rectangle is that when three square sections are removed, the remainder is another rectangle with the same proportions as the first.

Proof that b/(a-3b) is the same as a/b.:
If the long side of the remaining rectangle is 1, the short side is (3 + √13)/2 - 3.
1 / ((3 + √13)/2 - 3) =
1 / ((3 + √13)/2 - 6/2) =
1 / ((-3 + √13) /2)=
2/(-3 + √13) =
2( √13+3)/( √13-3)( √13+3) =
(2√13+6)/( 13-9) =
(3+√13)/2