Green Rectangle

In an earlier blog I questioned the assumption that the golden ratio or golden rectangle somehow contributes to an artwork's beauty, proportion or harmony. Since then it occurred to me that the golden rectangle might not be so special if you could show that other rectangles have similar properties.

I now propose an alternative to the golden rectangle, which I call the green rectangle. Instead of a rectangle whose side lengths are in the golden ratio, that is, approximately 1:1.618, I propose a rectangle whose side lengths are in the ratio of approximately 1:2.414, the green ratio.

Two quantities (positive numbers), a and b, are said to be in the golden ratio if (a+b)/a = a/b. I propose that two quantities, a and b, be in the green ratio if (a+b)/(a-b) = a/b. If we define this ratio as χ, the Greek letter chi, this leads to:
χ² - 2χ - 1 = 0

The only positive solution to this equation is:
χ = 1 + √2, or 2.414 (approximately).

Here's the calculation:

(a+b)/(a-b) = a/b = χ

The right equation shows that a = bχ, which can be substituted in the left part, giving:

(bχ + b)/(bχ - b) = bχ/b

Canceling b yields:

(χ + 1)/(χ - 1) = χ

Multiplying both sides by (χ - 1) and rearranging terms leads to:

χ² - 2χ - 1 = 0

The only positive solution to this quadratic equation is:

χ = 1 + √2 = approximately 2.414

A green rectangle is a rectangle whose side lengths are in the green ratio. I call this the green rectangle because it is leaner than the rather squat golden rectangle. Stood vertically, a green rectangle is taller, thinner, more like the ideal modern figure. Projecting the short side to a square base yields a tall box with a smaller footprint, as well.


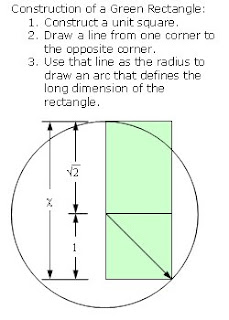
A not so distinctive feature of the golden rectangle is that when a square section is removed, the remainder is another rectangle with the same proportions as the first. Similarly, a feature of the green rectangle is that when two square sections are removed, the remainder is another green rectangle with the same proportions as the first.

Proof:
The long side of the remaining rectangle is 1 and the short side is 1 + √2 - 2.
1 / (1 + √2 - 2) =
1 / (-1 + √2) =
(-1 - √2)(1) / (-1 - √2)(-1 + √2) =
(-1 - √2) / (1 - √2 + √2 - 2) =
(-1 - √2) / -1 =
1 + √2

Double square removal can be repeated infinitely, which leads to an approximation of what I will call the "green spiral", similar to a golden spiral. Compared to a golden spiral, a green spiral is stretched, being made from quarter-ellipses, rather than quarter-circles. At any rate, using quarter-circles to generate a spiral is actually called a Fibonacci spiral, and only approximates a golden spiral. Perhaps a green spiral approximates a hyperbolic spiral — the math is beyond me. [Add a drawing of a green spiral and a hyperbolic spiral (with a=?) around the same center point.]

I don't deny that the golden rectangle is aesthetically pleasing. However, I don't think there's any proof that a connection exists between the math of the golden ratio and the beauty of a regular rectangle with proportions not too wide, not too thin.