The first twelve of an infinite series of rectangles

In my previous blogs I showed that the golden rectangle is not so distinctive in its feature that when a square section is removed, the remainder is another rectangle with the same proportions as the first. Similarly, a feature of the "green rectangle" that I described is that when two square sections are removed, the remainder is another green rectangle with the same proportions as the first. This can be carried on, infinitely I assume, so that there exist rectangles that when 3, 4, 5, etcetera, square sections are removed, the remainder is another rectangle with the same proportions as the first.

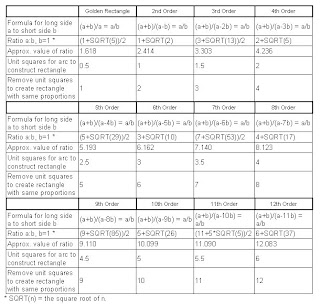
Each of these series of rectangles can be described by a formula or ratio of long side to short side, similar to the golden ratio. The golden ratio can be expressed algebraically as:
(a+b)/a = a/b, where a is the long side and b is the short.
The rectangles with similar features can be described algebraically simply by subtracting an integer number of short sides from the denominator of the right side of the equation.

Here are features of the first twelve such rectangles, starting with the golden rectangle.


Construction of an 8th order rectangle:


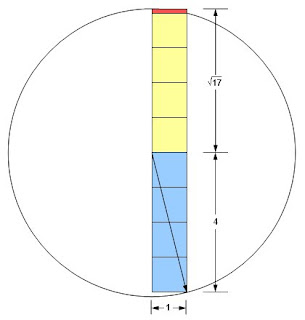
An 8th order rectangle with a short side of one has a long side of 4 plus the square root of 17. The ratio of long side to short side is therefore approximately 8.1231056. Removing 8 unit squares leaves the red rectangle, which has a short side of approximately 0.1231056 and a long side of 1. The new rectangle ratio of long side to short side is therefore approximately 1/0.1231056 or 8.123107.