Solution to fractional rectangles

In a previous blog I proposed a problem: to find the formulas (ratios for the long to short sides) for rectangles that are generated in a different series. That is, the golden rectangle is constructed by drawing a line across a half unit square. So, what are the formulas for a series of rectangles constructed by first drawing a line across a third, then a fourth, a fifth, a sixth, etcetera, of a unit square?

What I found was a series constructed by drawing a line across a fourth, eighth, sixteenth, etcetera, of a unit square. Here is a table of what I call the second through eighth order fractional rectangles, with the golden rectangle being the first order.

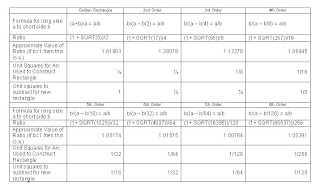
These rectangles have the following features in common with the golden rectangle:
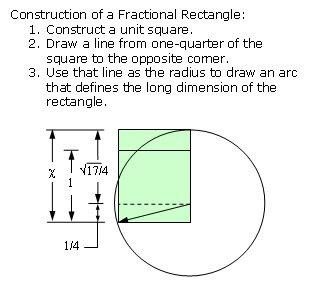
1. Simple construction. The rectangles can be constructed with a straightedge and compass. This is done by starting with a square and drawing a line across a fraction of the square. That line is used as a radius to draw an arc that defines the height of the rectangle.
2. Simple formula. Maybe not as simple as the golden ratio. The golden ratio is expressed algebraically as:
(a+b)/a = a/b
The second order fractional rectangle ratio is expressed as:
b/(a – b/2) = a/b
Each successive fractional rectangle in the series has a similar formula, the 2 being increased to 4, 8, 16, 32, etcetera.
3. Simple generation of rectangles spirally in from an original rectangle. When a simple fraction if a unit square is removed, the remainder is another rectangle with the same proportions as the first. Removal of the same fraction of a unit square can be repeated infinitely, which leads to spiral-like image.