The Rectangles Paper
Table 1. First Series Rectangles
Table 2. Second Series Rectangles
I've completed a draft of the paper, The Golden Rectangle — One Rectangle in a Continuum of Infinitely Many Similar Rectangles.
I'll now be preparing a tool to configure and print versions of the spirals.
Monday, November 26, 2007
Sunday, November 25, 2007
Saturday, November 24, 2007
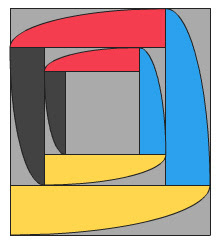
Second Series Rectangle, Spiral Example
This is the first example of a second series rectangle rendered with its "spiral". This is a "2nd order, fractional unit" rectangle. That means that the ratio of long side to short side is b/(a-b/24). The ratio of a/b is (1 + √65)/8, or approximately 1.13278. A "zero order, fractional unit" rectangle is the same as the golden rectangle.
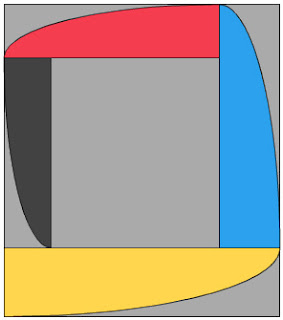

First Series Rectangle, Spiral Example
This is the first example of a new series rectangle rendered with its "spiral". This is a "1st order, multiple unit" rectangle. That means that the ratio of long side to short side is (a+b)/(a-b). The ratio of a/b is 1 + √2, or approximately 2.414213. A "zero order, multiple unit" rectangle is the same as the golden rectangle.

Friday, November 23, 2007
An Infinity of Rectangles
On the day before Thanksgiving, I finally posted "The Golden Rectangle — One Rectangle in a Continuum of Infinitely Many Similar Rectangles".
Now I'll be working on a Flash program to render the spirals that I can create with the new rectangles. The new spirals will be similar to the golden spiral. However, unlike approximations of a logarithmic spiral, they'll be elongated, or flattened looking.
Now I'll be working on a Flash program to render the spirals that I can create with the new rectangles. The new spirals will be similar to the golden spiral. However, unlike approximations of a logarithmic spiral, they'll be elongated, or flattened looking.
Monday, November 5, 2007
Solution to fractional rectangles
In a previous blog I proposed a problem: to find the formulas (ratios for the long to short sides) for rectangles that are generated in a different series. That is, the golden rectangle is constructed by drawing a line across a half unit square. So, what are the formulas for a series of rectangles constructed by first drawing a line across a third, then a fourth, a fifth, a sixth, etcetera, of a unit square?
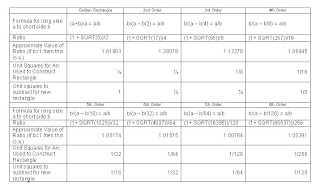
What I found was a series constructed by drawing a line across a fourth, eighth, sixteenth, etcetera, of a unit square. Here is a table of what I call the second through eighth order fractional rectangles, with the golden rectangle being the first order.
These rectangles have the following features in common with the golden rectangle:
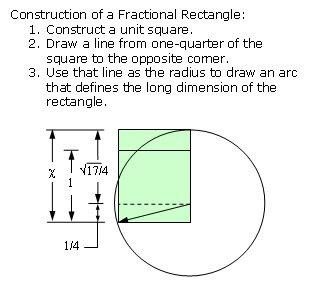
1. Simple construction. The rectangles can be constructed with a straightedge and compass. This is done by starting with a square and drawing a line across a fraction of the square. That line is used as a radius to draw an arc that defines the height of the rectangle.
2. Simple formula. Maybe not as simple as the golden ratio. The golden ratio is expressed algebraically as:
(a+b)/a = a/b
The second order fractional rectangle ratio is expressed as:
b/(a – b/2) = a/b
Each successive fractional rectangle in the series has a similar formula, the 2 being increased to 4, 8, 16, 32, etcetera.
3. Simple generation of rectangles spirally in from an original rectangle. When a simple fraction if a unit square is removed, the remainder is another rectangle with the same proportions as the first. Removal of the same fraction of a unit square can be repeated infinitely, which leads to spiral-like image.
What I found was a series constructed by drawing a line across a fourth, eighth, sixteenth, etcetera, of a unit square. Here is a table of what I call the second through eighth order fractional rectangles, with the golden rectangle being the first order.

These rectangles have the following features in common with the golden rectangle:
1. Simple construction. The rectangles can be constructed with a straightedge and compass. This is done by starting with a square and drawing a line across a fraction of the square. That line is used as a radius to draw an arc that defines the height of the rectangle.
2. Simple formula. Maybe not as simple as the golden ratio. The golden ratio is expressed algebraically as:
(a+b)/a = a/b
The second order fractional rectangle ratio is expressed as:
b/(a – b/2) = a/b
Each successive fractional rectangle in the series has a similar formula, the 2 being increased to 4, 8, 16, 32, etcetera.
3. Simple generation of rectangles spirally in from an original rectangle. When a simple fraction if a unit square is removed, the remainder is another rectangle with the same proportions as the first. Removal of the same fraction of a unit square can be repeated infinitely, which leads to spiral-like image.

West Coast art history
Portland was an excellent place to be this weekend for expanding my knowledge of West Coast art history. I saw Morgan Neville's Cool School on Friday at the Northwest Film Center. Neville was there to comment on the film. Tom Marioni gave a talk at Reed College on Saturday. I was very pleasantly surprised that much of the work he showed clicked with me. Finally, Kathan Brown of Crown Point Press gave a talk at PAM on Sunday.
Subscribe to:
Comments (Atom)